Equations for Distrust and Naivety

Using the trust functional (see Marginal potential) we can define the trust coefficient for a potential distribution over Value outcomes $p(v)$ as:

For a frame $\phi$ and an inclusion-candidate (person/thing) $x$, let the ultimate and subjective marginal shifts in Trust be:

Then, distrustful toward $x$ in frame $\phi$ is defined as:

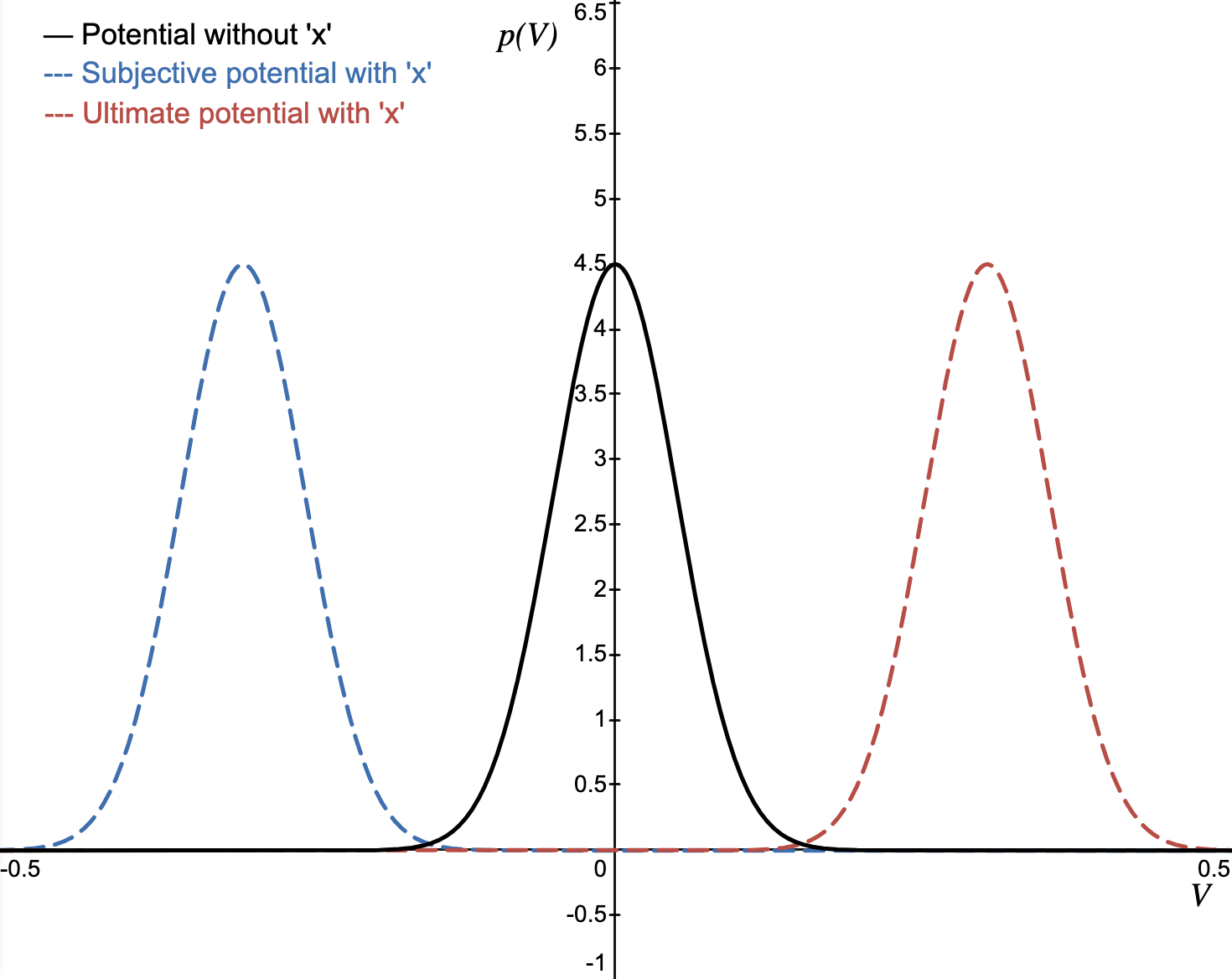
Degree of systematic pessimism—how much the subject underestimates x’s positive contribution to Potential relative to reality (0 means calibrated). In the following graph, the ultimate marginal shift is in trust is positive (+1), but the subjective marginal shift in trust is negative (-1). Plugging this into the equation gives us $\frac{1}{2} \max(0, 1 - (-1)) / 2 = 1$, or maximum level of distrust.

And naive about $x$ in frame $\phi$ is defined as:

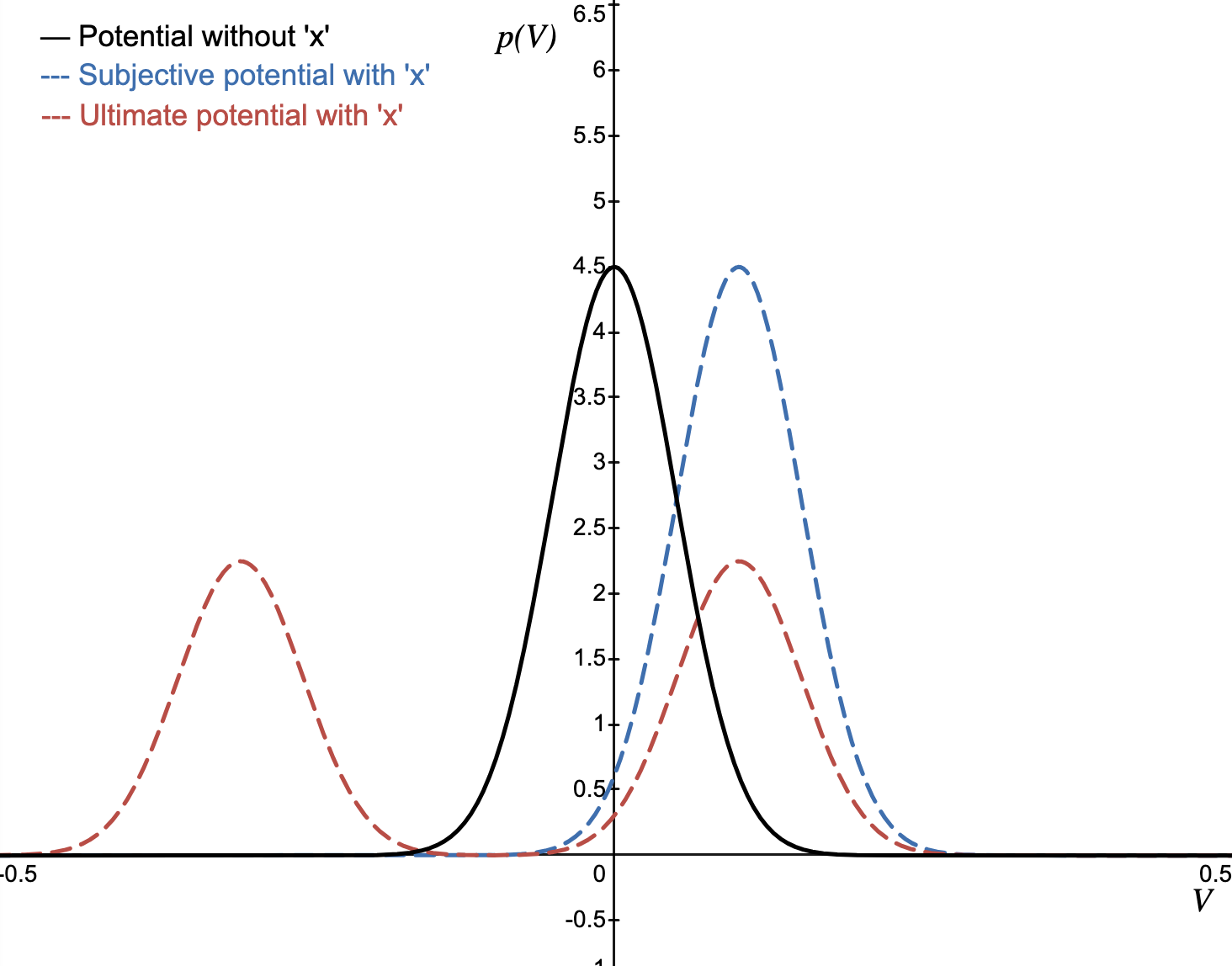
Degree of systematic optimism—how much the subject overestimates x’s positive contribution to potential relative to reality (0 means calibrated). If we plug in the numbers for the following graph, ignoring the tiny sections of the right humps that reach into the negative Value, we see that the subjective mass has shifted positive by 1, and the ultimate mass hasn't shifted (0), and so the result is $\frac{1}{2} \max(0, 1 - (-0)) = 0.5$ naive. If the ultimate mass had shifted all the way toward the negative side, the subject would be maximally naive.

A general expression with no specific x: with $T_\phi=A_T[p_\phi]$ and $T_\phi^{*}=A_T[p_\phi^{*}]$, define the signed trust bias $B_\phi=T_\phi^{*}-T_\phi$, then

These are the frame-level expressions for distrust and naivety.