Trust

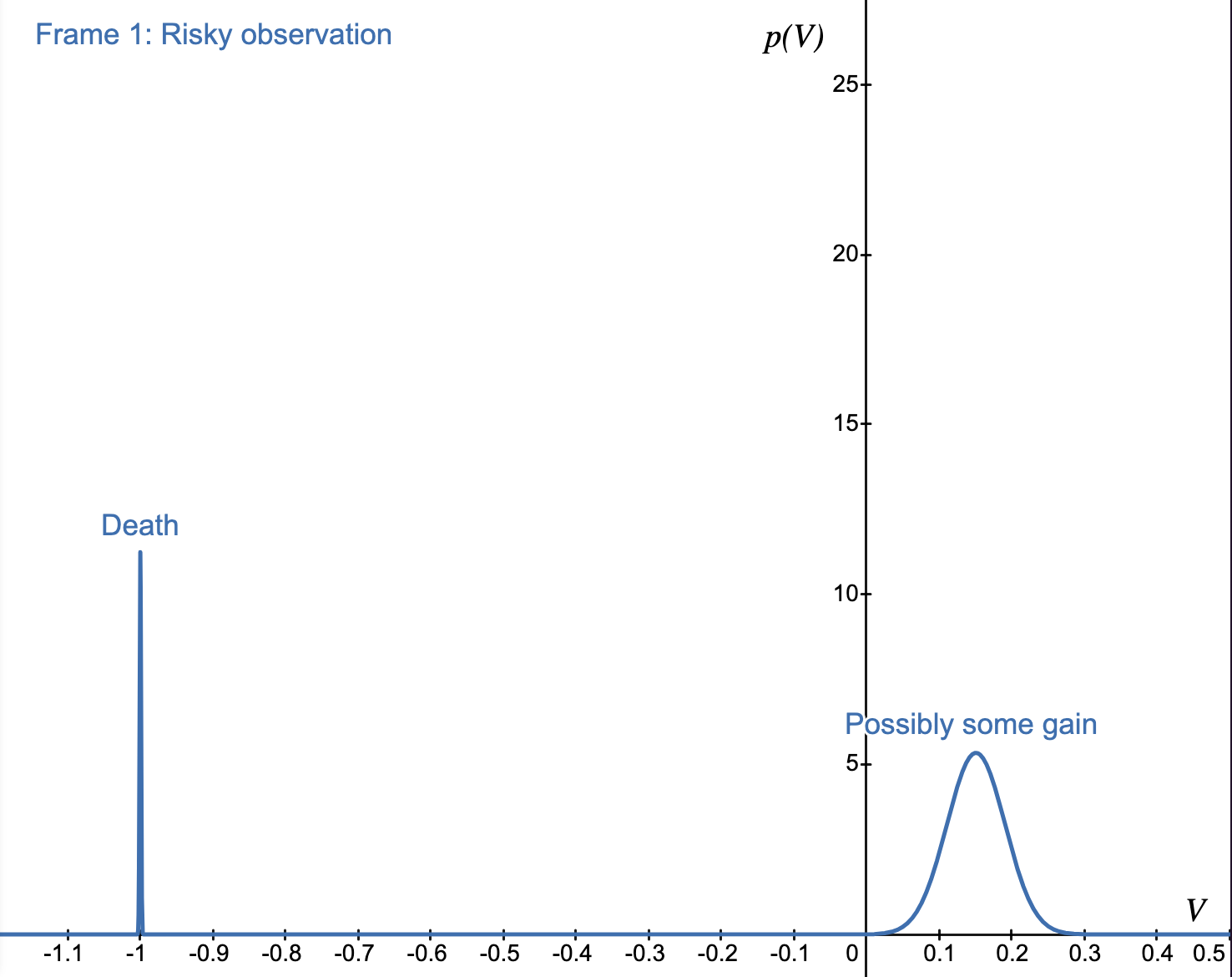
The essence of the feeling of trust is the knowledge or belief that the future will be good. Feelings can be described by the concept of Potential, which is the metaphysical and phenomenological entity that informs the feeling. The higher the potential, the greater the tension between what is and what could be, and the greater the intensity of the feeling. The shape of the feeling is determined by the probability density function $p(V)$ of Value outcomes, as in the following example where there's 5% chance of death (negative Value) and 95% chance of moderate gain (positive Value):

Although this probability density function is continuous, different aspects of this shape can be abstracted from it and articulated mathematically. These abstractions are the different names of feelings we know intuitively. Different feelings serve as different guides to Action, so even though our phenomenological experience of feelings is continuous and vague, our minds can abstract relevant signals that inform our decisions and determine how we act.

The feeling of trust is one of the simplest abstractions. If the subjectively perceived Potential of our frame lies on the positive side, we feel that things will turn out well, and we feel trust. If it lies on the negative side, we feel a feeling of distrust. The perceived feeling of Trust corresponds to how much of the subjective mass of $p(V)$ lies on the positive side.

Mathematically, we can extract a specific aspect from $p(V)$ by defining a summary functional. Trust functional is defined by:

$A_T[p]\;=\;\Pr_{p}(V>0)\;-\;\Pr_{p}(V<0)\;\in[-1,1],$

which is exactly the measurement of the probability density mass right or left of the y-axis. $Pr_{p}(V>0)$ asks how much of the mass is positive (in the graph above it's 0.95), and $Pr_{p}(V<0)$ asks how much mass is negative (0.05). Subtracting one from the other gives us the value of trust = 0.90.

Another intuitive feeling or experience is associating trust with some entity: to feel trust in someone or something. Like trusting your car, or trusting a person you know well. To get from a feeling of trust to this particular association of trust in $x$, it's only necessary to observe the difference between the two frames: your baseline or default frame, and the frame with $x$ included. If the inclusion of $x$ in your frame shifts the mass to the right, that means the inclusion $x$ was positive, and you trust it in this situation or frame. If the mass shifts to the left, it means the inclusion of $x$ was negative, and you don't trust it in this situation. This is explained in greater depth in Marginal potential.

A “thing” $x$ transforms the frame, and thus the distribution $p_\phi \to p_\phi^x$, so that we can define the marginal potential of $x$ in frame $\phi$, under $A$ functional as:

$\boxed{P_\phi^{A}(x)=A\left[p_\phi^x\right]-A\left[p_\phi\right]}$

Using our trust functional $A_T$, we can use this equation to arrive at the values for marginal trust or "trust in x".

Trust is a very simple abstraction over the potential distribution $p(V)$. It ignores the magnitude of the potential (how good things will turn out), and just looks at how much of the mass is positive vs negative. This checks out intuitively: If we know that a car is 100% reliable and will get us to our destination in our current frame of driving, it doesn't matter whether it's the best car or a low-end car, we feel complete trust in it. There may be other emotions overlaid on top of this base feeling of trust that pick out different aspects of the potential distribution, and create a more nuanced and layered feeling, but the feeling of trust will be the one that makes us decide whether to use this car or not. The best car that's not our own might not give us the same feeling of trust as our own car that we know inside-out.