Potential

In my article Understand I describe the hypothesis that our natural languages have an embedded mathematical matrix, which encodes the meaning of our concepts. Our way of using language reflects an intuitive understanding of this underlying structure, even though we may not be aware of the structure itself.

For example, when we say someone or something “has potential” what do we mean? We mean there is something promising within them or it—a hidden or undeveloped power, talent, or possibility that could manifest under the right conditions. In simpler terms, potential is the possibility or capacity for something to become greater, better, or more fully developed in the future, i.e., higher Quality.

More generally, potential is experienced as the tension between what is and what could be, between where we are, and where we could end up. A physics analogy is the potential energy of an object which increases with the distance from the ground. Similarly, if the difference in terms of Quality between what is and what could be is large, there is more potential.

The what is and what could be is modeled by a frame $\;\phi=\bigl(s_0,\;\pi_\phi\bigr)$ where $s_0$ represents the current state, and $\;\pi_\phi$ represents the probability distribution over future states, the chance of any one state manifesting.

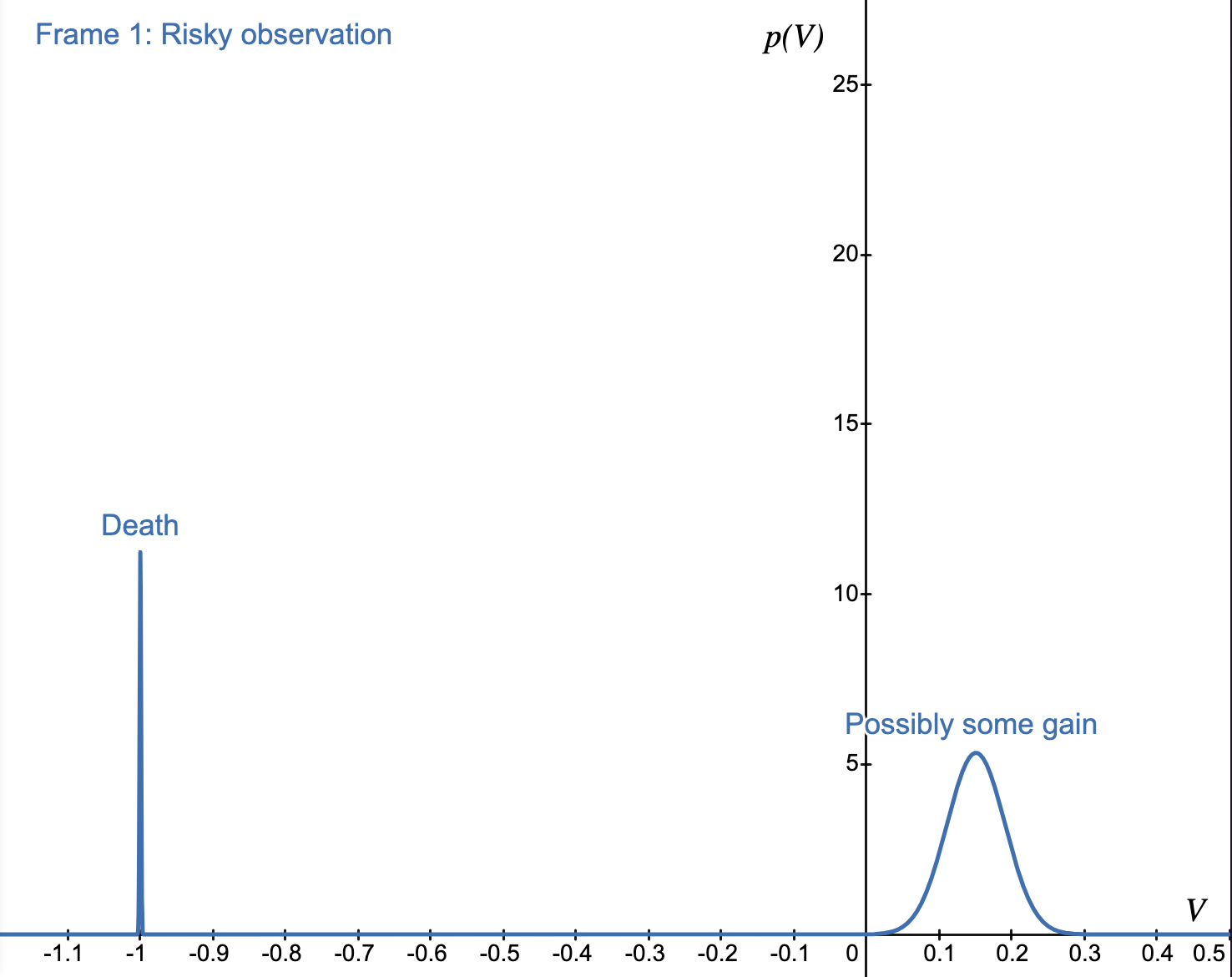
Consider a lookout point over a cliff [^1] and imagine two different frames of observing the landscape. If one stands at the edge of the cliff to get a better view, practice courage, or any other well-intentioned reason, the experienced potential is very different from the scenario of standing at a safe distance from the edge—there's danger and possibility of sudden death. There's an intuitive way to visualize this experience by plotting a probability density function (PDF) of Value outcomes.

Whereas a single Value outcome is the difference between one state from the probability distribution $\;\pi_{\phi}$ and the initial state $V = Q(s) - Q(s_0)$, when this is done for all states, and the states are weighed by the probability of them occurring, we get a clear representation of potential:

Here's how to read this graph: Value (V) on the x axis is normalized between -1 and 1, which signifies the span from the worst possible outcome (in this case death) to the best possible outcome. (What ultimately matters is the shape of the curve, not absolute values). The area under the curve represents probability. The narrow spike on the left has 0.05 of total area and hence 5% chance of occurring. The right hump has 0.95 area and 95% of occurring. The total area under the curve of a PDF always sums up to 1 (or 100% probability).

Together the two humps model the feeling experienced in this situation. Negative Value outcomes map to a negative feeling, whereas positive Value outcomes map to positive feeling. In this situation there is a "mixed feeling" of both negative and positive outcomes. The more the Value outcome approaches the extremes -1 or 1, the more the feeling can be intense: in this case death represents the ultimate negative outcome. I said "can be intense", because it's proportional to the probability of the Value outcome: if Value outcome of death has approximately 0% chance, it won't be taken as seriously as when it has 5% chance, which is the case above. The variance of the hump represents the degree of uncertainty: in the case falling from a cliff, it essentially means a certain death, whereas potential of falling down the stairs might have a more spread out hump (high chances of low to moderate injury, and a low chance of death). The positive part of potential on the right is more uncertain in terms of Value outcome: something good is expected to happen, but it might be only marginally good at values close to 0, or really good at values close to 0.3.

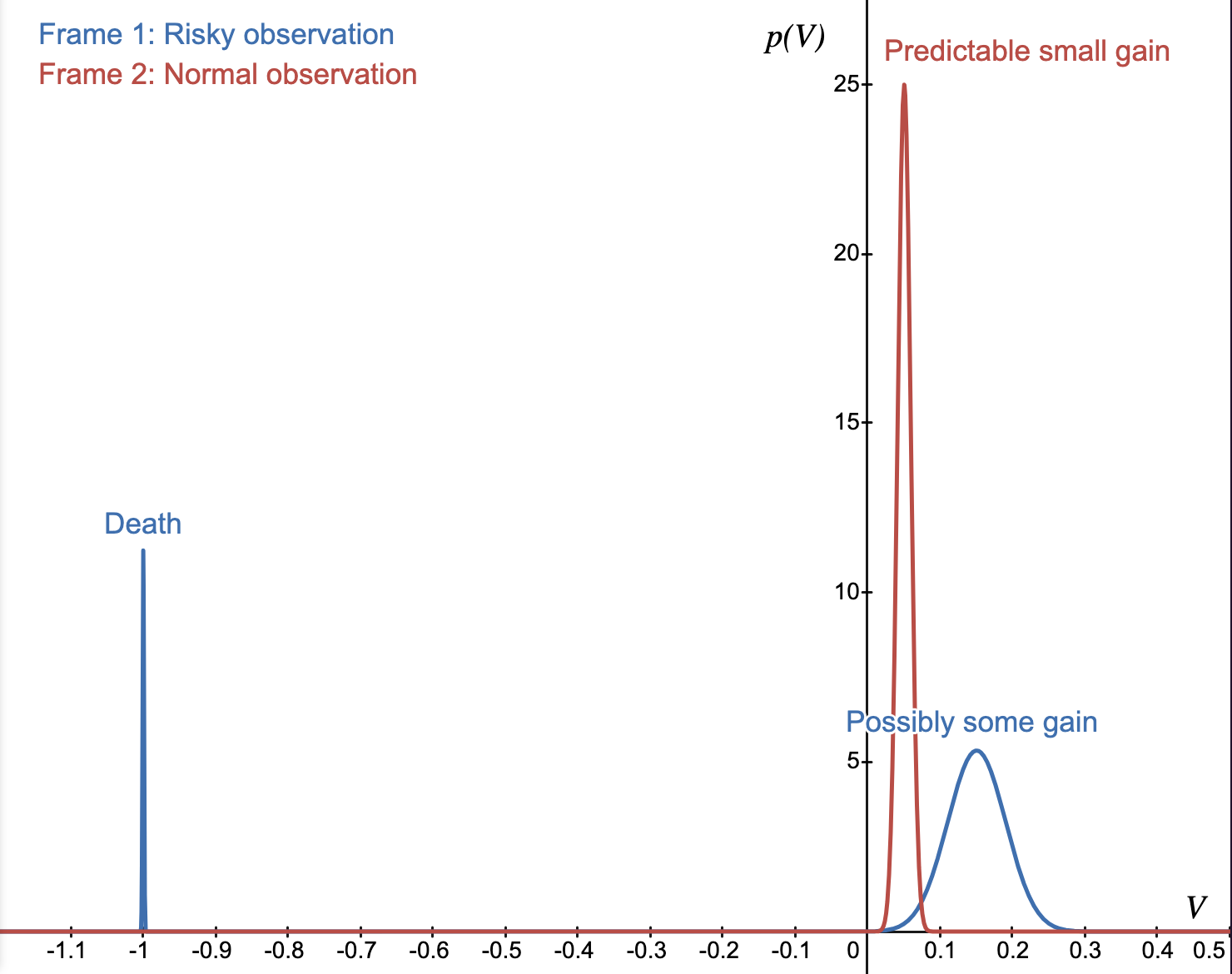
Let's analyze one more frame.

The second frame $\phi_2$ has a fairly predictable future $\pi_{\phi_2}$ with no risk of dying, and only a marginal gain afforded by the view. There's only one hump centered around V = 0.05. The hump is fairly narrow, which means that the range of outcomes is more certain: we are expecting a mildly pleasant experience with no surprises.

Carl Jung defined the function of feeling as perception of Value. Potential is composed of a distribution of Value outcomes, which are informed by subject's frame—the current state or what is, the expectations of the future or what could be. Our perception of different kinds of potential, different distributions of outcomes, is what informs the feelings we experience.

Probability density function is a way to model the feeling in a flexible and informative way. With a sufficiently complex function we can model more complex feelings. The goal at present is not to create a taxonomy of feeling, but to create a mathematical framework for understanding human Action.

What I omitted before for simplicity is that subject's evaluations of those states matter as much as expectations. In his Maps of Meaning lectures, Jordan Peterson often makes a point that "We are not expectation machines—we don't act based on what we expect; we act based on what we value". A depressed person will judge $s_{death}$ to be a better state than $s_0$ and will jump off the cliff. A healthy person will judge $s_{death}$ to be a worse state, and will get away from the edge. Because their frame is different, their evaluations are different. Different evaluations mean different experience of potential, and hence different actions. [^2]

We are both emotional agents and rational agents. Our actions are shaped by both what we value and what we expect.

To summarize: we can think of potential as a distribution of Value outcomes $p_\phi(v)$. The shape of the distribution maps the experienced feeling, the felt potential of variety of things that could happen in a situation.

From this definition of potential as a felt experience that reflects the possible outcomes of our current Aim, we can also arrive at the notion of potential that we perceive in a person or a thing. This is where we started this note: "What does it mean for someone or something to have potential?" We'll call this "potential in a thing" marginal potential.

[1]: Jordan Peterson's thoughts on potential inspired much of this thinking. In his Ted talk he gives metaphysical and perceptual arguments for why this concept is fundamental to reality: Potential: Jordan Peterson at TEDxUofT.

[2]: A further layer of complexity is that evaluations are based on subjective judgements of Quality, which can be aligned with the ultimate Quality or not. There's a difference in the "feeling tone" between a suicidal person that jumps off a cliff intending to die, and an ignorant person that jumps off the cliff expecting to fly. The first person's values are misaligned, the second person is merely ignorant of cause-effect relations of the material world (misaligned expectations).